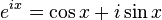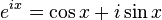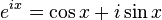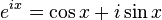Papildyta:
Apskaiciuti ribas, gal atsiras kam smalsu ir sita uzdavinuka issprest
o sita gauso ir kramerio metodais reikia ispresti, kramerio metodu issprendziau,o gauso vel gi nesuprantu
QUOTE(egliuchiux @ 2011 11 29, 22:38)
o is kur 4 stulpelyje - matricoje ar kaip pavadinti atsirado antra eilute 0 -3 3 9 18 ??
maniau kad sukeitėte 4 eilute su antra.. bet tada ne -3 butu o -7
sorry.. man tik idomu.. noriu prisiminti
maniau kad sukeitėte 4 eilute su antra.. bet tada ne -3 butu o -7
sorry.. man tik idomu.. noriu prisiminti
Ten be reikalo taip padariau, nes tai nėra susije su sprendimo, naudojant Gauso metodą, peripetijomis. Kadangi kalba turėjo eiti išskirtinai tik apie pastarąjį būdą, siūlau nuo minėtos vietos įsivaizduoti -7 (o ne -3) - išvados ir atsakymas nuo to nepasikeis
-----
QUOTE(Sunkissed @ 2011 11 29, 22:27)
Del gauso metodo....kaip nusprendziat is kokio skaiciaus reikia dauginti,kokius veiksmus reikia atlikti ?
1 -1 1 -3
-6 1 1 -21
8 -4 -1 14
1 -1 1 -3
-6 1 1 -21
8 -4 -1 14
Pradžiai neabejotinai prie 2-os eilutės 6 kartus pridėti 1-ą eilutę, tada iš 3-ios eilutės 8 kartus atimti 1-ą eilutę. Ir jau bus pusė darbo.
QUOTE(Dėdė Pranas @ 2011 11 30, 00:00)
Ten be reikalo taip padariau, nes tai nėra susije su sprendimo, naudojant Gauso metodą, peripetijomis. Kadangi kalba turėjo eiti išskirtinai tik apie pastarąjį būdą, siūlau nuo minėtos vietos įsivaizduoti -7 (o ne -3) - išvados ir atsakymas nuo to nepasikeis
aišku kad niekas neaišku
kartais skaitydama Jūsų postus tokia buka jaučiuosi.. nors nesu jei nesunku gal pagelbėsit su tais kompleksiniais skaičiais
QUOTE(Sunkissed @ 2011 11 29, 22:55)
...
Papildyta:
Apskaiciuti ribas, gal atsiras kam smalsu ir sita uzdavinuka issprest
...
Papildyta:
Apskaiciuti ribas, gal atsiras kam smalsu ir sita uzdavinuka issprest
...
Reikia dvinarį vardiklyje pakelti kvadratu. Tada ir skaitiklį, ir vardiklį padalinti iš x kvadratu.
Tai kaip ir akimirksniu duos atsakymą, turint galvoje, kad A/x ar B/(x kvadratu) yra nykstami dydžiai (čia A, B - kokie nors paprasti fiksuoti skaičiai).
-----
QUOTE(egliuchiux @ 2011 11 29, 20:56)
Ateinu ir aš su prašymu. deja matematikos nebeturiu bet vis atsiranda prašančių pagalbos.. ka galiu ta padedu bet su šitais neteko man niekur susidurti. gal kas gali išspresti? 
Che che, aš pamenu, kad netolimoje praeityje jums jau rašiau kelis paprastus sprendimus, susijusius su kompleksinių skaičių prasme, tai dabar jau dvejoju
Šiaip pavyzdžiui pirmame tereikia sudauginti panariui ir tada vietoj (i kvadratu) parašyti (-1) - neįkvepiantis uždavinukas.
Kiti gal keliais žodžiais nepaaiškinami, bet tarkim trečias matosi mintinai pagal (Wikipedia paveikslėlis):
Jei nepraeis noras, galėsiu rytoj vakare parašyti likusius du, nes dabar jau planuoju eiti pamiegoti, pailsėti prieš rytojų.
Gero vakaro.
QUOTE(Dėdė Pranas @ 2011 11 30, 00:10)
Reikia dvinarį vardiklyje pakelti kvadratu. Tada ir skaitiklį, ir vardiklį padalinti iš x kvadratu.
Tai kaip ir akimirksniu duos atsakymą, turint galvoje, kad A/x ar B/(x kvadratu) yra nykstami dydžiai (čia A, B - kokie nors paprasti fiksuoti skaičiai).
Tai kaip ir akimirksniu duos atsakymą, turint galvoje, kad A/x ar B/(x kvadratu) yra nykstami dydžiai (čia A, B - kokie nors paprasti fiksuoti skaičiai).
oo.. ir aš supratau..
ir tada atsakymas gaunasi 3/4? tada gal mane užvesite ant kelio su c varijantu. viska išsprendžiau o va C nesumastau nuo ko pradėt
QUOTE(egliuchiux @ 2011 11 30, 00:20)
oo.. ir aš supratau.. ir tada atsakymas gaunasi 3/4?
tada gal mane užvesite ant kelio su c varijantu. viska išsprendžiau o va C nesumastau nuo ko pradėt
ir tada atsakymas gaunasi 3/4? tada gal mane užvesite ant kelio su c varijantu. viska išsprendžiau o va C nesumastau nuo ko pradėt
Taip, tokia ir yra ta riba.
C eilutėje galima skaitiklį bei vardiklį dalinti iš 3^x (3 pakelta x-uoju laipsniu) ir tolimesnė mąstymo logika bus analogiška.
P.S. Paredagavau ankstesnį savo komentarą.
QUOTE(Dėdė Pranas @ 2011 11 30, 00:10)
Che che, aš pamenu, kad netolimoje praeityje jums jau rašiau kelis paprastus sprendimus, susijusius su kompleksinių skaičių prasme, tai dabar jau dvejoju
Šiaip pavyzdžiui pirmame tereikia sudauginti panariui ir tada vietoj (i kvadratu) parašyti (-1) - neįkvepiantis uždavinukas.
Kiti gal keliais žodžiais nepaaiškinami, bet tarkim trečias matosi mintinai pagal (Wikipedia paveikslėlis):
Jei nepraeis noras, galėsiu rytoj vakare parašyti likusius du, nes dabar jau planuoju eiti pamiegoti, pailsėti prieš rytojų.
Gero vakaro.
taip taip.. taciau as neperkandau tu skaiciu ir preita karta draugui niekuom nepadejau
prisipazystu kad as visai ju nesuprantu ir nesu susidūrusi todel ir prasiau ne paaiskinimo o kas netingi kad išsprestu 
taip naglai ane o dėl ribų tai ačiū
dabar supratau ta C 
Papildyta:
QUOTE(Dėdė Pranas @ 2011 11 30, 00:10)
tereikia sudauginti panariui ir tada vietoj (i kvadratu) parašyti (-1) - neįkvepiantis uždavinukas.
Kiti gal keliais žodžiais nepaaiškinami, bet tarkim trečias matosi mintinai pagal (Wikipedia paveikslėlis):
Jei nepraeis noras, galėsiu rytoj vakare parašyti likusius du, nes dabar jau planuoju eiti pamiegoti, pailsėti prieš rytojų.
Gero vakaro.
Kiti gal keliais žodžiais nepaaiškinami, bet tarkim trečias matosi mintinai pagal (Wikipedia paveikslėlis):
Jei nepraeis noras, galėsiu rytoj vakare parašyti likusius du, nes dabar jau planuoju eiti pamiegoti, pailsėti prieš rytojų.
Gero vakaro.
hm.. sudauginau panariui ir gavau :
2/9 + 7/9i-4/9i^2
o kudie vietoj i^2 riek rasyt -1? ir ka rasyt vietoj i. ar cia su kompleksiniai skaiciais tokios taisykles?
man jau idomu
pagal ta paveiksleli tai gaunasi (e^35i) ^ -12?? na e pakeltas 35i ir dar pakeltas -12??
ir kas toliau
QUOTE(Dėdė Pranas @ 2011 11 30, 01:00)
-----
Pradžiai neabejotinai prie 2-os eilutės 6 kartus pridėti 1-ą eilutę, tada iš 3-ios eilutės 8 kartus atimti 1-ą eilutę. Ir jau bus pusė darbo.
padariau tuos veiksmus
gavau..
1 -1 1 |-3
0 -5 7 |-39
0 4 -9 |38
o ka toliau...
QUOTE(Sunkissed @ 2011 11 30, 01:22)
Kadangi ieškote tendencijų, kurios tiktų daugeliu atvejų, galima dabar būtų elgtis pagal tradicines taisykles.
Kaip anksčiau minėjau rašydamas apie Gauso metodą: "reikia, jog žemiau 2-os eilutės 2-ame stulpelyje būtų nuliai". Taigi galite 2-ą eilutę dauginti iš nelabai elegantiško daugiklio 0,8 ir tada ją panariui pridėti prie 3-ios eilutės. Liks tam tikra prasme tokia "laiptuota" matrica ir uždavinys bus beveik išspręstas - beliks iš paprastos sistemos išrašyti nežinomųjų reikšmes
-----
QUOTE(egliuchiux @ 2011 11 30, 00:37)
...
hm.. sudauginau panariui ir gavau :
2/9 + 7/9i-4/9i^2
o kudie vietoj i^2 riek rasyt -1? ir ka rasyt vietoj i. ar cia su kompleksiniai skaiciais tokios taisykles?
man jau idomu
...
hm.. sudauginau panariui ir gavau :
2/9 + 7/9i-4/9i^2
o kudie vietoj i^2 riek rasyt -1? ir ka rasyt vietoj i. ar cia su kompleksiniai skaiciais tokios taisykles?
man jau idomu
...
Jau beveik turite atsakymą savo rankoje!
Savaime i yra tiesiog skaičius ir, nors turi įdomių savybių, daugiau niekaip nesusiprastina, taigi dėmuo 7i/9 toks ir liks. Lygiai taip pat liktų ir 7e/9 ar 7*PI/9 - daugiau juk greičiausiai nebebūtų, ką gražaus nuveikti
Tuo tarpu aš pakartosiu ankstesnį paveikslėlį, kuris labai svarbus:
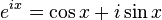
Manau, jog nesunku suvokti, kad galima parašyti taip:
bet tada juk tinka svarbioji formulė t.y.:
Štai ir įrodėme. Šiaip kompleksinis skaičius nereiškia nieko daugiau, kaip kad du dėmenys, kurių vienas paprastas, o kitas padaugintas iš i.
-----
QUOTE(egliuchiux @ 2011 11 30, 00:37)
...
pagal ta paveiksleli tai gaunasi (e^35i) ^ -12?? na e pakeltas 35i ir dar pakeltas -12?? ir kas toliau
pagal ta paveiksleli tai gaunasi (e^35i) ^ -12?? na e pakeltas 35i ir dar pakeltas -12??
ir kas toliau Kai keliame laipsniu du kartus, laipsnių rodikliai juk sudauginami. Tada grįžtama atgal į pradinę formą (kosinusą ir sinusą).
2) Iš dalies trigonometrinė forma jau pažįstama pagal Wikipedia paveikslėlį.
Jai prilyginus turim:
Buvo sulygintos paprastos dalys ir dalys, kurios padaugintos iš i.
Išsprendus lygčių sistemėlę nesunkiai gaunami r ir fi (graikiškos abėcėlės raidė), kurie ir nurodo trokštamą trigonometrinę formą.
4) Vietoj x^2 pažymim t ir sprendžiam kvadratinę lygtį grynai mokykliniu būdu:
Ir bus beveik baigta, pabaigą paminėsiu vėliau
QUOTE(Dėdė Pranas @ 2011 11 30, 18:56)
Kadangi ieškote tendencijų, kurios tiktų daugeliu atvejų, galima dabar būtų elgtis pagal tradicines taisykles.
Kaip anksčiau minėjau rašydamas apie Gauso metodą: "reikia, jog žemiau 2-os eilutės 2-ame stulpelyje būtų nuliai". Taigi galite 2-ą eilutę dauginti iš nelabai elegantiško daugiklio 0,8 ir tada ją panariui pridėti prie 3-ios eilutės. Liks tam tikra prasme tokia "laiptuota" matrica ir uždavinys bus beveik išspręstas - beliks iš paprastos sistemos išrašyti nežinomųjų reikšmes
Kaip anksčiau minėjau rašydamas apie Gauso metodą: "reikia, jog žemiau 2-os eilutės 2-ame stulpelyje būtų nuliai". Taigi galite 2-ą eilutę dauginti iš nelabai elegantiško daugiklio 0,8 ir tada ją panariui pridėti prie 3-ios eilutės. Liks tam tikra prasme tokia "laiptuota" matrica ir uždavinys bus beveik išspręstas - beliks iš paprastos sistemos išrašyti nežinomųjų reikšmes
1 -1 1 |-3
0 -5 7 |-39
0 0 -3,4|6,8
gavau tokia matrica, ir as galeciau as paskutine eilute padalinti is 3,4 ,tada gautusi sveiki skaiciai, nes israsius man siek tiek nesamone gaunasi, x3= -0,5 , x2= 0,14085
arba as kazka ne taip darau...
QUOTE(Sunkissed @ 2011 11 30, 20:03)
Visa tai atitinka šią sistemą:
3-ioje eilutėje egzistuoja tik vienas nežinomasis, taigi akivaizdžiai galima išreikšti, kad jis lygus -2. Tuo pasinaudojus 2-oje eilutėje (įstačius -2) irgi lieka vienas nežinomasis, kuris nesunkiai išreiškiamas. Tokiu būdu ("keliaujant" iš apačios į viršų) galima suskaičiuoti juos visus.
Štai ir mokėsite gan universalų būdą
